الأربعاء، 30 ديسمبر 2015
الثلاثاء، 29 ديسمبر 2015
الثلاثاء، 15 ديسمبر 2015
السبت، 12 ديسمبر 2015
التروس
التـِـرْسْ أو المسنن أو الترس المسنن هو جزء ميكانيكي يوجد داخل آليات نقل الحركة ووظيفته نقل الحركة الدورانية للترس
(المركب على محور) إلى ترس أو جزء ميكانيكي آخر. ويختلف الترس عن الطارة
في أن الترس عبارة عن عجلة دائرية بها بروزات (أسنان أو دندانجات[1]) تتعاشق مع أسنان الترس الآخر مما يسمح
للقوة بالانتقال التام بدون انزلاق. وحسب تصميم التروس وترتيبها يمكن للتروس نقل
القوى بسرعاتوعزوم مختلفة أو في اتجاهات مختلفة من مصدر
الحركة الأساسي. والتروس مفيدة جداً في الآلات البسيطة. في معظم
الحالات يتعاشق الترس مع ترس آخر ولكن الترس يمكن أن يعشق مع أي جزء ميكانيكي له
نفس شكل الأسنان كما في الحركة البسيطة الجريدة المسننة والترس.
ومن أهم مميزات التروس أنها تكون بأحجام غير متساوية (أقطار) يمكن تجميعها معًا للحصول على فائدة
آلية وبذلك فإن السرعة الدورانية والعزم للترس الثاني يختلف عنهما في الترس
الأول. داخل أي آلة، المصطلح "ترس" أيضا يشير إلى ترتيبة واحدة معينة من
التروس بترتيبات أخرى (مثل"الترس الأول"). مثل هذه الترتيبات تعطى كنسب
عدد أسنان تروس أو كنسب أقطار التروس كوحدات. ومصطلح "ترس" يستخدم أيضًا
للأجزاء غير المسننة التي تؤدي نفس الغرض. وكان الجزري أول من شرح استخدام
الترس.
تاريخ التروس
تظهر التروس في مخطوطاتعلم
الحيل التي كتبها علماء مسلمون استنادًا
إلى علوم الإغريق وطوروا «حيل» خاصة
بهم.
كانت الحبال ومواد أخرى مصنوعة من الأخشاب تستخدم قديمًا في آليات بسيطة لنقل الحركة
مثل البكَّرات
الرافعة، لكن لا أحد
يعرف على وجه الدقة أين أو متى بدأ استخدام العجلات، ومع أن الأدب الصيني القديم
والأدب اليوناني والتركي والدمشقي قد أشاروا كثيرًا إلى التروس إلا أنهم لا يقدمون
الكثير من التفاصيل.
وتعد آلية أنتيكيثيرا أقدم الآليات
المتبقية من العصور القديمة، وهي حاسبة آلية فلكية تعود إلى ما بين 150-100 ق.م،
وتتألف مما لا يقل عن ثلاثين ترسًا برونزيًا أسنانهم مثلثة الشكل.
ومع أن هذه الآلية موغلة في القدم إلا أنها تعد متقدمة جدًا من الناحية التقنية
مثل نظام
التروس التداويري "epicyclic gearing" التي كانت
تعد من اختراعات القرن التاسع عشر قبل اكتشاف هذه الآلية. بعض الاقتباسات من شيشرون تبين أن أنتيكيثيرا لم
تكن الآلية الوحيدة من نوعها في ذلك الوقت، وإنما كان هنالك، على الأقل، آليتان
أخرتان تشبهانها، قام بتصنيع إحداهما أرشميدس في حين قام بوسيدونيوس بتصنيع الأخرى،
ومن الجدير بالذكر أن أرشميدس يعد واحدًا من مخترعي التروس، إذ ينسب إليه أنه أول
من صمم مجموعة إدارة بترس دودي "Worm drive".
قد حافظت الصين على عدة أمثلة لآلات تعتمد في تصميمها على التروس، ومن الأمثلة
على ذلك عربة التمثال المشير إلى الجنوب (120-250م)، وهي عربة بها آلية من تروس
فرقية "Differential
gears" تربط بين عجلاتها وتمثال آدمي
أعلى العربة يشير ذراعه إلى الجنوب، تعمل مجموعة التروس الفرقية على عقد ذراع
التمثال موجهًا دائمًا إلى الجنوب مهما تغير اتجاه العربة؛ إذ تساعد التروس الفرقية
على تحديد الفرق بين دوران عجلتي العربة ومن ثم تحديد دوران قاعدة العربة ثم تعوض
هذا الدوران بإدارة التمثال في الاتجاه الآخر، وهي بذلك تعمل عمل بوصلة لا مغناطيسية. قبل اختراع
هذه العربة بقليل وبالتحديد نحو سنة 50م توصل الصينيون لصناعة التروس اللولبية
"helical gear"
عن طريق النحت في الخشب، وقد عثر على أحد هذه التروس بمقبرة في مدينة شانسي الصينية "Shensi".
Helical gears
تروس اهليجية
أعلى: تشكيل متوازي
أسفل: تشكيل متقاطع
أعلى: تشكيل متوازي
أسفل: تشكيل متقاطع
صندوق تروس ذو
مرحلتين
صندوق التروس[2] أو المناول[3] أو علبة السرعة[4]آلةحركية تقوم بتقوية (أو تخفيف) عزم الدوران باستعمال
عدة تروس ذات أحجام مختلفة ينتج عنها تخفيض (أو رفع) سرعة الدوران. علماً
بأن 90% من صناديق التروس تعتبر مخفضة للسرعة وبالتالي هي تهتم بزيادة عزم الدوران في حين أن
10% منها يعتبر مخفض للعزم وبالتالي هي تهتم بزيادة السرعة، حيث أن عزم
الدوران يساوي القدرة مقسومة على سرعة الدوران.
·
استخدامه
تستعمل صناديق التروس
استعمالاً واسعاً في شتى التطبيقات الميكانيكية التي تعتمد في إنتاجها على توليد
عزم دوران مثلما في السيارات ٍ ويقوم صندوق
التروس بمهمة زيادة سرعة الدوران أو
تخفيضها عن طريق توصيل
الحركة من المحرك إلى المحور إلى العجلات
. وهو يعتبر الوسيلة المثلى لتوليد العزم أو زيادة السرعة الدورانية في آلات كثيرة
. كما انه لا يكاد يخلو مصنع أو منشأة صناعية من استخدام صناديق التروس ولو في
أبسط أشكالها. ونحن نستخدم صناديق التروس في حياتنا اليومية العامة متمثلة في وسائل النقل المختلفة مثل السيارات و الحافلات و الشاحناتوالطائرات وحتى الدراجات وغيرها.
يأتي التحكم في السرعة عن طريق منظومة لتروس ذات أحجام مختلفة .
مثال: إذا كان الترس الدوار كبيرا بالنسبة إلى ترس صغير ، فإن دورة واحدة
للترس الكبير تتسبب في عدة دورات للترس الصغير ؛ هذا يعتمد على عدد اسنان الترس
الكبير والترس الصغير. في حالتها هذه يدور الترس الصغير عدة دورات أثناء دوران
الترس الكبير دورة واحدة (أي تزداد السرعة) . وبالعكس إذا كان الترس الصغير هو
المتحرك ويدير الترس الكبير ؛ في تلك الحالة تحدث تهدئة للسرعة ؛ حيث أن عدة دورات
للترس الصغير تتسبب في دورة واحدة للترس الكبير . وهذا هو مبدأ عمل صندوق التروس.
العمر الافتراضي
يحدد عمر صندوق التروس يحدد بالحمل على أسنان الترسوعدد دورات الترس الذي يكوّن مركـّبة (component) للمناول. حيث أن
لكل مناول ترسي سرعة مصممة عليه مسبقاً؛ إذا تجاوزها المستخدم فإن العمر
الافتراضي لصندوق التروس يصبح أقل مما هو مصمم عليه. كما أن بعض صناديق
التروس ترفق عند شرائها برسوم بيانية يمكن بها
حساب العمر الافتراضي لها في ظروف تشغيل مختلفة.
الترس هو عجلة مسننة ،
يحتوي محيطها على عدد من الاسنان ذات شكل خارجي .ويمكن تشكيل الاسنان بطريقة القطع
بواسطة سكاكين تفريز لها حدود قاطعة بشكل الفجوات بين الاسنان. وتستعمل التروس
بصورة عامة في نقل الحركة الدورانية من محور الى اخر وخاصة عندما تكون المسافة بين
هذه المحاور صغيرة نسبياً . وتتم عملية نقل الحركة هذه دون انزلاق وذلم لتداخل
اسنان احد التروس في فجوات الترس الاخر . ويمكن ً تحويل الحركة الدورانية الى حركة
مستقيمة وذلك بأستعمال ترس وقضيب مسنن ( الجريدة المسننة والترس المعشق معها).
انواع التروس
يمكن تصنيف التروس الى
ثلاثة مجاميع هي:
1. التروس الاسطوانية : تستعمل هذه التروس عادة في نقل الحركة بين المحاور المتوازية التي تقع في مستوي واحد . وتنقسم هذه التروس عادة من حيث اتجاه الاسنان بالنسبة لمحور الترس الى تروس اسطوانية مستقيمة الاسنان ، والى تروس اسطوانية مائلة الاسنان.
2. التروس المخروطية : تستعمل هذه التروس بصورة رئيسية في نقل الحركة الدورانية بين المحاور المائلة المتقطعة (اي المحاور غير المتوازية والتي تقع في مستوى واحد).
أما الشكل الاساسي لهذه التروس فهو المخروط الناقص . وتنقسم هذه التروس من حيث شكل الاسنان الى:
تروس مخروطية مستقيمة الاسنان ، والى تروس مخروطية مائلة الاسنان.
3. التروس اللولبية : تستعمل هذه التروس في نقل الحركة بين المحاور التي لاتتقاطع في الفراغ ، اي التي لاتقع في مستوى واحد، وتضم هذه المجموعة التروس اللولبية الحلزونية والتروس البريمية (الحلزون).
الشكل ادناه يوضح بعض انواع التروس .
1. التروس الاسطوانية : تستعمل هذه التروس عادة في نقل الحركة بين المحاور المتوازية التي تقع في مستوي واحد . وتنقسم هذه التروس عادة من حيث اتجاه الاسنان بالنسبة لمحور الترس الى تروس اسطوانية مستقيمة الاسنان ، والى تروس اسطوانية مائلة الاسنان.
2. التروس المخروطية : تستعمل هذه التروس بصورة رئيسية في نقل الحركة الدورانية بين المحاور المائلة المتقطعة (اي المحاور غير المتوازية والتي تقع في مستوى واحد).
أما الشكل الاساسي لهذه التروس فهو المخروط الناقص . وتنقسم هذه التروس من حيث شكل الاسنان الى:
تروس مخروطية مستقيمة الاسنان ، والى تروس مخروطية مائلة الاسنان.
3. التروس اللولبية : تستعمل هذه التروس في نقل الحركة بين المحاور التي لاتتقاطع في الفراغ ، اي التي لاتقع في مستوى واحد، وتضم هذه المجموعة التروس اللولبية الحلزونية والتروس البريمية (الحلزون).
الشكل ادناه يوضح بعض انواع التروس .
ا.ترسي اسطواني ذو
اسنان مستقيمة (ترس اسطواني عدل )
ب.تروس اسطوانية معتدلة مسننة خارجياً
جـ- تروس اسطوانية معتدلة مسننة داخلياً (تروس حلقية)
د- جريدة مسننة والترس المعشق معها
هـ- تروس مخروطية مسننة خارجاً
و- تروس مخروطية مسننة داخلياً
ز- تروس مخروطية تاجية
حـ- تروس حلزونية الاسنان
ط- تروس لولبية الاسنان
ي- البريمة (الحلزونية) والترس الحلزوني المعشق معها .
ب.تروس اسطوانية معتدلة مسننة خارجياً
جـ- تروس اسطوانية معتدلة مسننة داخلياً (تروس حلقية)
د- جريدة مسننة والترس المعشق معها
هـ- تروس مخروطية مسننة خارجاً
و- تروس مخروطية مسننة داخلياً
ز- تروس مخروطية تاجية
حـ- تروس حلزونية الاسنان
ط- تروس لولبية الاسنان
ي- البريمة (الحلزونية) والترس الحلزوني المعشق معها .
مصطلحات أسنان التروس:
1. دائرة القمة:Addendum Circle
هى الدائرة التى تمر
بقمم أسنان الترس أى أنها تمثل السطح الخارجى لقرص الترس.
قطر دائرة القمه = قطر
دائرة الخطوة + 2× ارتفاع نصف السن العلوي
= ق + 2 × م وبما ان ق
= م × ع
= م × ع + 2 × م
= م × ( ع + 2 )
قطردائرة القمه = المودول × ( عدد اسنان الترس +2 ) ملم
= م × ع + 2 × م
= م × ( ع + 2 )
قطردائرة القمه = المودول × ( عدد اسنان الترس +2 ) ملم

2. دائرة القاع: Dedendum Circle
هى الدائرة التى تمر
بجذر الفراغ بين أسنان الترس.
قطر دائرةالقاع= قطر دائرة الخطوة – 2× ارتفاع نصف السن السفي
= ق – 2 ×1.2 × م وبما ان ق = م × ع
= م × ع - 2,4 × م
قطر دائرة القاع= المودول × (عدد اسنان الترس – 2.4) ملم
قطر دائرةالقاع= قطر دائرة الخطوة – 2× ارتفاع نصف السن السفي
= ق – 2 ×1.2 × م وبما ان ق = م × ع
= م × ع - 2,4 × م
قطر دائرة القاع= المودول × (عدد اسنان الترس – 2.4) ملم
هى دائرة وهمية تقع بين
دائرة القمة ودائرة القاع، ويتم عندها تعشيق أسنان الترس القائد والمنقاد..
قطر دائرة الخطوة = المودول × عدد اسنان الترس
ق = م × ع
قطر دائرة الخطوة = المودول × عدد اسنان الترس
ق = م × ع
4. الخطوة الدائرية
(خد) : C.P.) Circular Pitch)
هي الدائرة التي يتم
تقسيم اسنان الترس على محيطها بخطوات معينة ثابتة . اي ان جميع اسنان الترس تقع
على محيط الترس وعلى مسافات متساوية بين بعضها وتسمى هذه المسافات المتساوية
بالخطوة الدائرية كما يمكن تعريفها هى المسافة بين نقطتين متماثلتين على سنين
متتاليتين مقاسة على دائرة الخطوة.
الخميس، 10 ديسمبر 2015
المدى
المدى
في الإحصاء، يطلق اسم المدى على طول أصغر مجال يضم جميع عناصر البيانات. ويتم حسابه بطرح العينة الصغرى من العينة الكبرى ويعطى فكرة كأحد مقاييس التشتت.
في الإحصاء، يطلق اسم المدى على طول أصغر مجال يضم جميع عناصر البيانات. ويتم حسابه بطرح العينة الصغرى من العينة الكبرى ويعطى فكرة كأحد مقاييس التشتت.
فالجدول التالي يبين درجات 30 طالب في مادة الرياضيات والمطلوب المدى لهذه الدرجات
| الفئات | 24 – 28 | 29 – 33 | 34 – 38 | 39 – 43 | 44 – 48 | 48 – 52 |
| التكرار | 3 | 4 | 7 | 6 | 8 | 2 |
الحد الأعلى للفئة العليا = 52
الحد الأدنى للفئة الدنيا = 24
المدى = 52 – 24 = 28
توزيع طبيعي متعدد المتغيرات
في نظرية الاحتمال والإحصاء يُعتبر التوزيع الطبيعي متعدد المتغيرات أو توزيع غاوسي متعدد المتغيرات تعميم (متغير واحد) لـتوزيع احتمالي طبيعي من أحادي الأبعاد إلى أعلى الأبعاد. أحد التعريفات المحتملة هو أن المتجه العشوائي يكون k-متغير يوزع بصورةٍ طبيعية، لو تحتوي كل تركيبة خطية من مكونات k على توزيع طبيعي وحيد المتغير. ومع ذلك, تستمد أهميتها بشكلٍ رئيسي من مبرهنة النهاية المركزية متعددة المتغيرات. يُستخدم غالبًا التوزيع الطبيعي متعدد المتغيرات لوصف- على الأقل تقريبًا- أي مجموعة (محتملة) من المتغيرات العشوائية المرتبطة بالقيمة الحقيقية حيث يتجمع كل واحد منها حول متوسط القيمة.

التعريف
المتجه العشوائي x = (X1, …, Xk)' يُقال إنه يحتوي على التوزيع الطبيعي متعدد المتغيرات، إذا استوفى الشروط الموازية التالية.[1]
- كل تركيب خطي من مكوناته Y = a1X1 + … + akXk يتم توزيعه بشكل طبيعي. هذا يعني, لأي متجه ثابت a ∈ Rk, المتغير العشوائي Y = a′x لديه توزيع طبيعي وحيد المتغير.
- يوجد هناك متغير ℓ-عشوائي z, الذي تُعتبر مكوناته معيار مستقل للمتغيرات العشوائية الطبيعية, a k-متغير μ,و a k×ℓ مصفوفة A, مثل x = Az + μ. هنا ℓ يكون بمثابة صف مصفوفة التغاير Σ = AA′. خاصة في حالة الصف الكامل, انظر المقطع أدناه عن التفسير الهندسي.
- يوجد k-متجه μ وk×k مصفوفة Σ متناظر ذو قيمة غير سالبة محددة -, بحيث تكون الدالة المميزة لـx

يسمح لمصفوفة التغاير أن تكون مفردة (في الحالة التي لا يوجد للتوزيع المتكافىء كثافة). كثيرًا ما تظهر تلك الحالة في الإحصاء، فعلى سبيل المثال, تظهر في توزيع متجه اختلاف القيم المتبقية في انحدار المربعات الصغرى العادية. يجب ملاحظة أن Xi لا يكونوا مستقلين غالبًا، ويمكن النظر إليهم كنتيجة لتطبيق المصفوفة A على مجموعة من متغيرات غاوسي المستقلة z.
الوسيط للبيانات الغير مبوبة
في الرياضيات وفي علم الإحصاء، الوسيط أو الوسط (بالإنجليزية: Median) هو الرقم الذي يفصل النصف الأعلى من العينة أو المجتمع عن النصف الأقل بحيث يتساوى على طرفه عدد القيم بعد ترتيبها تصاعدياً.
فإذا كان عدد هذه القيم فردياً فالوسيط هو الرقم النصفي الذي يقسم هذه القيم،
أما إذا كان عدد القيم زوجياً فالوسيط هو الوسط الحسابي لمجموع الرقمين الوسيطيين.
مثال: إذا كانت العينة: 1 3 4 6 8 فالوسيط هو الرقم 4
مثال 2 : إذا كانت العينة : 1 2 3 4 5 6 7 فالوسيط هو الرقم 4
مثال 2 : إذا كانت العينة : 1 2 3 4 5 6 7 فالوسيط هو الرقم 4
مثال: إذا كانت العينة 1 3 4 5 7 9 فالوسيط يساوي 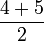
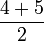
مثال 2 : إذا كانت العينة 1 2 3 4 5 6 فالوسيط يساوي 

المنوال للبيانات الغير مبوبة
المنوال
أمثلة
لو فرضنا القيم التالية :
(a,b,e,r,a,c,f,a,v,b,r,a)
يكون المنوال (mode) هنا:هو القيمة الأكثر
تكرارا وهي (a)
مثال :
لو فرضنا
أن لدينا الأعداد (4,2,4,1,9,7,4,6,4)المنوال في هذه الحالة = 4لأنه الأكثر تكرارا
في حالة :
1-
لايوجد قيمة متكررة بين القيم ففي هذه الحاله
نكتب لا يوجد منوال ولا يصح ابدا ان نكتب المنوال=0 لان 0 هو ايضا قيمة
أمثلة
اوجد المنوال :
(1,4,9,6,0,7)
يكون المنوال هنا = لا
يوجد منوال لانه لا يوجد قيمة متكررة
المتوسط الحسابي للبيانات غير المبوبة
المتوسط الحسابي :
هو قيمة تتجمع حولها قيم مجموعة ويمكن من خلالها الحكم على بقية قيم المجموعة، فتكون هذه القيمة هي الوسط
الحسابي.
يكون
المتوسط الحسابي محصورًا دائمًا بين أكبر وأصغر عدد في العيّنة.
إنّ
المتوسط الحسابي لمجموعة أعداد
هو النقطة على محور الأعداد التي مجموع أبعادها
عن كل نقطة في المجموعة يساوي صفر.
حساب المتوسط الحسابي :
1-
نجمع القيم المراد ايجاد الوسط الحسابي لها
2-
نقسم مجموع القيم على عددها
مثال :
إذا كانت لديك ثلاثة أرقام، فمن أجل حساب المتوسط الحسابي، تقوم
بالعملية التالية:
ــــــــــــــــــــــــــــــــــــــــــــ
مثال
اوجد المتوسط الحسابي لكلا من :
a , b ,o , y , r,
يكون المتوسط هنا
ـــــــــــــــــــــــــــــــــــــــــــــــــــــ
مثال :
اوجد المتوسط الحسابي لكلا من
1,3,5,7,9,12,5,8,10,4
يكون المتوسط الحسابي هنا هو
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
وهكذا نكون تعلمنا كيفية ايجاد
المتوسط الحسابي للبيانات الغير
مبوبة
والسلام عليكم ورحمة الله وبركاته
الاشتراك في:
التعليقات (Atom)


